GEOMETRIA ANALÍTICA
Dados os vetores  e o ângulo formado entre estes vetores é de
e o ângulo formado entre estes vetores é de  , encontre o produto interno
, encontre o produto interno  entre os vetores
entre os vetores  .
.





Encontre a equação geral para parábola de vértice V(5, 3) e foco F(2, 3).
y2 - 4x + 12y + 44 = 0
y2 - 6x + 2 + 22 = 0
y2 + 12x – 6y - 51 = 0
y2 + 12x – 4y - 52 = 0
y2 - 4x – 12y - 48 = 0
Encontre o vértice oposto a B, no paralelogramo ABCD, para A(-3, -1), B(4, 2) e C(5, 5).
D(2, -1)
D(2, 1)
D(1, 2)
D(2, -2)
D(-2, 2)
Considerando os conceitos básicos sobre vetores enumere a 2ª coluna de acordo com a 1ª coluna.
I – Vetor nulo
( )Vetor resultado da soma de dois vetores de mesma direção e comprimento; com sentidos contrários.
II – Vetores iguais
( ) Sua subtração gera um vetor nulo.
III – Vetores opostos
( ) Sua adição gera um vetor nulo.
IV – Versor
( ) Intensidade, comprimento ou módulo de um vetor.
V – Vetor unitário
( ) Possuem mesma direção.
VI – Norma
( ) Vetor cujo o comprimento é uma unidade, independente da direção ou sentido.
VII – Vetores eqüipolentes
( ) É um vetor unitário, sempre obtido pela divisão de um vetor por sua norma.
Assinale a alternativa que expressa a sequência correta.
I,II,III,V,VI,IV,VII
I,II,III,VI,VII,V,IV
I,II,III,V,VII,VI,IV
I,III,V,VII,II,IV,VI
I,II,III,V,VII,IV,VI
Encontre a medida dos semieixos, os focos e a excentricidade da elipse x2 + y2 = 9.
a = 3; b = 3; F1(3, 0) e F2(-3, 0); e = 1/3
a = 3; b = 3; F1(-3, 0) e F2(3, 0); e = 0
a = -3; b = -3; F1(3, 0) e F2(0, 3); e = 1/3
a = 3; b = 3; F1(0, 0) e F2(0, 0); e = 0
a = 9; b = 9; F1(0, 0) e F2(0, 0); e = 1/9
Determine os focos e a excentricidade da elipse 9x2 + 5y2 – 45 = 0.
F1(-3,0) e F2(5,0), e = √5/2
F1(-2,0) e F2(2,0), e = 2/√5
F1(2,0) e F2(0,-2), e = 2/√5
F1(0,-2) e F2(0,2), e = 2/3
F1(-5,0) e F2(3,0), e = 2/5
Identifique a equação da superfície hiperbolóide de uma folha de centro possui coordenadas (3, -1, -4) cujo eixo encontra-se paralelo ao eixo Oy.
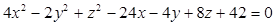
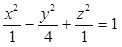
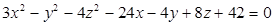
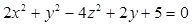
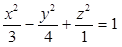
Dado o ponto A(2, 3, -4) e o vetor v = (1, -2, 3), determine as equações vetoriais e paramétricas da reta r que passa por A e tem a direção de v.





Uma embalagem de vidro com um líquido de alta qualidade nutricional possui forma esférica e 6 cm de raio. Considerando que o líquido na embalagem contém apenas 1/3 de seu volume total e o consumo diário é de 10 ml, em quantos dias, aproximadamente, ele será consumido? Obs.: use π = 3,14
Encontre a equação geral para parábola de vértice V(5, 3) e foco F(2, 3).
y2 - 4x + 12y + 44 = 0
y2 - 6x + 2 + 22 = 0
y2 + 12x – 6y - 51 = 0
y2 + 12x – 4y - 52 = 0
y2 - 4x – 12y - 48 = 0
Encontre o vértice oposto a B, no paralelogramo ABCD, para A(-3, -1), B(4, 2) e C(5, 5).
D(2, -1)
D(2, 1)
D(1, 2)
D(2, -2)
D(-2, 2)
Considerando os conceitos básicos sobre vetores enumere a 2ª coluna de acordo com a 1ª coluna.
I – Vetor nulo
( )Vetor resultado da soma de dois vetores de mesma direção e comprimento; com sentidos contrários.
II – Vetores iguais
( ) Sua subtração gera um vetor nulo.
III – Vetores opostos
( ) Sua adição gera um vetor nulo.
IV – Versor
( ) Intensidade, comprimento ou módulo de um vetor.
V – Vetor unitário
( ) Possuem mesma direção.
VI – Norma
( ) Vetor cujo o comprimento é uma unidade, independente da direção ou sentido.
VII – Vetores eqüipolentes
( ) É um vetor unitário, sempre obtido pela divisão de um vetor por sua norma.
Assinale a alternativa que expressa a sequência correta.
I,II,III,V,VI,IV,VII
I,II,III,VI,VII,V,IV
I,II,III,V,VII,VI,IV
I,III,V,VII,II,IV,VI
I,II,III,V,VII,IV,VI
Encontre a medida dos semieixos, os focos e a excentricidade da elipse x2 + y2 = 9.
a = 3; b = 3; F1(3, 0) e F2(-3, 0); e = 1/3
a = 3; b = 3; F1(-3, 0) e F2(3, 0); e = 0
a = -3; b = -3; F1(3, 0) e F2(0, 3); e = 1/3
a = 3; b = 3; F1(0, 0) e F2(0, 0); e = 0
a = 9; b = 9; F1(0, 0) e F2(0, 0); e = 1/9
Determine os focos e a excentricidade da elipse 9x2 + 5y2 – 45 = 0.
F1(-3,0) e F2(5,0), e = √5/2
F1(-2,0) e F2(2,0), e = 2/√5
F1(2,0) e F2(0,-2), e = 2/√5
F1(0,-2) e F2(0,2), e = 2/3
F1(-5,0) e F2(3,0), e = 2/5
Identifique a equação da superfície hiperbolóide de uma folha de centro possui coordenadas (3, -1, -4) cujo eixo encontra-se paralelo ao eixo Oy.
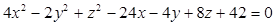
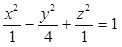
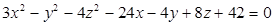
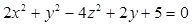
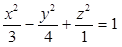
Dado o ponto A(2, 3, -4) e o vetor v = (1, -2, 3), determine as equações vetoriais e paramétricas da reta r que passa por A e tem a direção de v.





Uma embalagem de vidro com um líquido de alta qualidade nutricional possui forma esférica e 6 cm de raio. Considerando que o líquido na embalagem contém apenas 1/3 de seu volume total e o consumo diário é de 10 ml, em quantos dias, aproximadamente, ele será consumido? Obs.: use π = 3,14
y2 - 4x + 12y + 44 = 0
y2 - 6x + 2 + 22 = 0
y2 + 12x – 6y - 51 = 0
y2 + 12x – 4y - 52 = 0
y2 - 4x – 12y - 48 = 0
Encontre o vértice oposto a B, no paralelogramo ABCD, para A(-3, -1), B(4, 2) e C(5, 5).
D(2, -1)
D(2, 1)
D(1, 2)
D(2, -2)
D(-2, 2)
Considerando os conceitos básicos sobre vetores enumere a 2ª coluna de acordo com a 1ª coluna.
I – Vetor nulo
( )Vetor resultado da soma de dois vetores de mesma direção e comprimento; com sentidos contrários.
II – Vetores iguais
( ) Sua subtração gera um vetor nulo.
III – Vetores opostos
( ) Sua adição gera um vetor nulo.
IV – Versor
( ) Intensidade, comprimento ou módulo de um vetor.
V – Vetor unitário
( ) Possuem mesma direção.
VI – Norma
( ) Vetor cujo o comprimento é uma unidade, independente da direção ou sentido.
VII – Vetores eqüipolentes
( ) É um vetor unitário, sempre obtido pela divisão de um vetor por sua norma.
Assinale a alternativa que expressa a sequência correta.
I,II,III,V,VI,IV,VII
I,II,III,VI,VII,V,IV
I,II,III,V,VII,VI,IV
I,III,V,VII,II,IV,VI
I,II,III,V,VII,IV,VI
Encontre a medida dos semieixos, os focos e a excentricidade da elipse x2 + y2 = 9.
a = 3; b = 3; F1(3, 0) e F2(-3, 0); e = 1/3
a = 3; b = 3; F1(-3, 0) e F2(3, 0); e = 0
a = -3; b = -3; F1(3, 0) e F2(0, 3); e = 1/3
a = 3; b = 3; F1(0, 0) e F2(0, 0); e = 0
a = 9; b = 9; F1(0, 0) e F2(0, 0); e = 1/9
Determine os focos e a excentricidade da elipse 9x2 + 5y2 – 45 = 0.
F1(-3,0) e F2(5,0), e = √5/2
F1(-2,0) e F2(2,0), e = 2/√5
F1(2,0) e F2(0,-2), e = 2/√5
F1(0,-2) e F2(0,2), e = 2/3
F1(-5,0) e F2(3,0), e = 2/5
Identifique a equação da superfície hiperbolóide de uma folha de centro possui coordenadas (3, -1, -4) cujo eixo encontra-se paralelo ao eixo Oy.
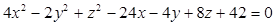
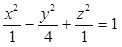
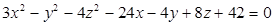
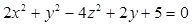
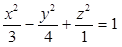
Dado o ponto A(2, 3, -4) e o vetor v = (1, -2, 3), determine as equações vetoriais e paramétricas da reta r que passa por A e tem a direção de v.





Uma embalagem de vidro com um líquido de alta qualidade nutricional possui forma esférica e 6 cm de raio. Considerando que o líquido na embalagem contém apenas 1/3 de seu volume total e o consumo diário é de 10 ml, em quantos dias, aproximadamente, ele será consumido? Obs.: use π = 3,14
D(2, -1)
D(2, 1)
D(1, 2)
D(2, -2)
D(-2, 2)
Considerando os conceitos básicos sobre vetores enumere a 2ª coluna de acordo com a 1ª coluna.
I – Vetor nulo
( )Vetor resultado da soma de dois vetores de mesma direção e comprimento; com sentidos contrários.
II – Vetores iguais
( ) Sua subtração gera um vetor nulo.
III – Vetores opostos
( ) Sua adição gera um vetor nulo.
IV – Versor
( ) Intensidade, comprimento ou módulo de um vetor.
V – Vetor unitário
( ) Possuem mesma direção.
VI – Norma
( ) Vetor cujo o comprimento é uma unidade, independente da direção ou sentido.
VII – Vetores eqüipolentes
( ) É um vetor unitário, sempre obtido pela divisão de um vetor por sua norma.
Assinale a alternativa que expressa a sequência correta.
I,II,III,V,VI,IV,VII
I,II,III,VI,VII,V,IV
I,II,III,V,VII,VI,IV
I,III,V,VII,II,IV,VI
I,II,III,V,VII,IV,VI
Encontre a medida dos semieixos, os focos e a excentricidade da elipse x2 + y2 = 9.
a = 3; b = 3; F1(3, 0) e F2(-3, 0); e = 1/3
a = 3; b = 3; F1(-3, 0) e F2(3, 0); e = 0
a = -3; b = -3; F1(3, 0) e F2(0, 3); e = 1/3
a = 3; b = 3; F1(0, 0) e F2(0, 0); e = 0
a = 9; b = 9; F1(0, 0) e F2(0, 0); e = 1/9
Determine os focos e a excentricidade da elipse 9x2 + 5y2 – 45 = 0.
F1(-3,0) e F2(5,0), e = √5/2
F1(-2,0) e F2(2,0), e = 2/√5
F1(2,0) e F2(0,-2), e = 2/√5
F1(0,-2) e F2(0,2), e = 2/3
F1(-5,0) e F2(3,0), e = 2/5
Identifique a equação da superfície hiperbolóide de uma folha de centro possui coordenadas (3, -1, -4) cujo eixo encontra-se paralelo ao eixo Oy.
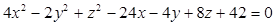
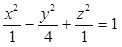
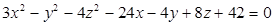
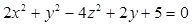
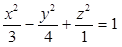
Dado o ponto A(2, 3, -4) e o vetor v = (1, -2, 3), determine as equações vetoriais e paramétricas da reta r que passa por A e tem a direção de v.





Uma embalagem de vidro com um líquido de alta qualidade nutricional possui forma esférica e 6 cm de raio. Considerando que o líquido na embalagem contém apenas 1/3 de seu volume total e o consumo diário é de 10 ml, em quantos dias, aproximadamente, ele será consumido? Obs.: use π = 3,14
I,II,III,V,VI,IV,VII
I,II,III,VI,VII,V,IV
I,II,III,V,VII,VI,IV
I,III,V,VII,II,IV,VI
I,II,III,V,VII,IV,VI
Encontre a medida dos semieixos, os focos e a excentricidade da elipse x2 + y2 = 9.
a = 3; b = 3; F1(3, 0) e F2(-3, 0); e = 1/3
a = 3; b = 3; F1(-3, 0) e F2(3, 0); e = 0
a = -3; b = -3; F1(3, 0) e F2(0, 3); e = 1/3
a = 3; b = 3; F1(0, 0) e F2(0, 0); e = 0
a = 9; b = 9; F1(0, 0) e F2(0, 0); e = 1/9
Determine os focos e a excentricidade da elipse 9x2 + 5y2 – 45 = 0.
F1(-3,0) e F2(5,0), e = √5/2
F1(-2,0) e F2(2,0), e = 2/√5
F1(2,0) e F2(0,-2), e = 2/√5
F1(0,-2) e F2(0,2), e = 2/3
F1(-5,0) e F2(3,0), e = 2/5
Identifique a equação da superfície hiperbolóide de uma folha de centro possui coordenadas (3, -1, -4) cujo eixo encontra-se paralelo ao eixo Oy.
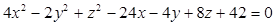
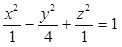
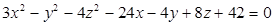
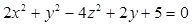
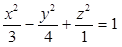
Dado o ponto A(2, 3, -4) e o vetor v = (1, -2, 3), determine as equações vetoriais e paramétricas da reta r que passa por A e tem a direção de v.





Uma embalagem de vidro com um líquido de alta qualidade nutricional possui forma esférica e 6 cm de raio. Considerando que o líquido na embalagem contém apenas 1/3 de seu volume total e o consumo diário é de 10 ml, em quantos dias, aproximadamente, ele será consumido? Obs.: use π = 3,14
a = 3; b = 3; F1(3, 0) e F2(-3, 0); e = 1/3
a = 3; b = 3; F1(-3, 0) e F2(3, 0); e = 0
a = -3; b = -3; F1(3, 0) e F2(0, 3); e = 1/3
a = 3; b = 3; F1(0, 0) e F2(0, 0); e = 0
a = 9; b = 9; F1(0, 0) e F2(0, 0); e = 1/9
Determine os focos e a excentricidade da elipse 9x2 + 5y2 – 45 = 0.
F1(-3,0) e F2(5,0), e = √5/2
F1(-2,0) e F2(2,0), e = 2/√5
F1(2,0) e F2(0,-2), e = 2/√5
F1(0,-2) e F2(0,2), e = 2/3
F1(-5,0) e F2(3,0), e = 2/5
Identifique a equação da superfície hiperbolóide de uma folha de centro possui coordenadas (3, -1, -4) cujo eixo encontra-se paralelo ao eixo Oy.
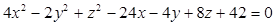
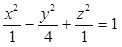
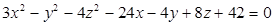
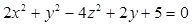
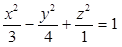
Dado o ponto A(2, 3, -4) e o vetor v = (1, -2, 3), determine as equações vetoriais e paramétricas da reta r que passa por A e tem a direção de v.





Uma embalagem de vidro com um líquido de alta qualidade nutricional possui forma esférica e 6 cm de raio. Considerando que o líquido na embalagem contém apenas 1/3 de seu volume total e o consumo diário é de 10 ml, em quantos dias, aproximadamente, ele será consumido? Obs.: use π = 3,14
F1(-3,0) e F2(5,0), e = √5/2
F1(-2,0) e F2(2,0), e = 2/√5
F1(2,0) e F2(0,-2), e = 2/√5
F1(0,-2) e F2(0,2), e = 2/3
F1(-5,0) e F2(3,0), e = 2/5
Identifique a equação da superfície hiperbolóide de uma folha de centro possui coordenadas (3, -1, -4) cujo eixo encontra-se paralelo ao eixo Oy.
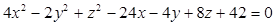
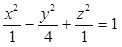
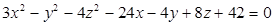
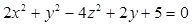
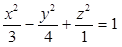
Dado o ponto A(2, 3, -4) e o vetor v = (1, -2, 3), determine as equações vetoriais e paramétricas da reta r que passa por A e tem a direção de v.





Uma embalagem de vidro com um líquido de alta qualidade nutricional possui forma esférica e 6 cm de raio. Considerando que o líquido na embalagem contém apenas 1/3 de seu volume total e o consumo diário é de 10 ml, em quantos dias, aproximadamente, ele será consumido? Obs.: use π = 3,14
![]()
![]()
![]()
![]()
![]()